- Part one introduces the notion of path symmetry: a property of uniform-cost grid maps which can significantly slow down search.
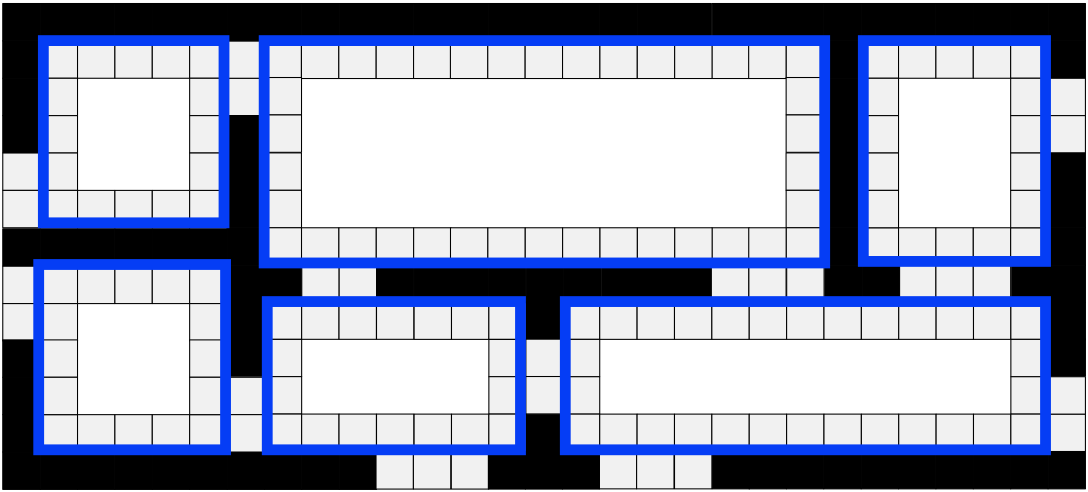
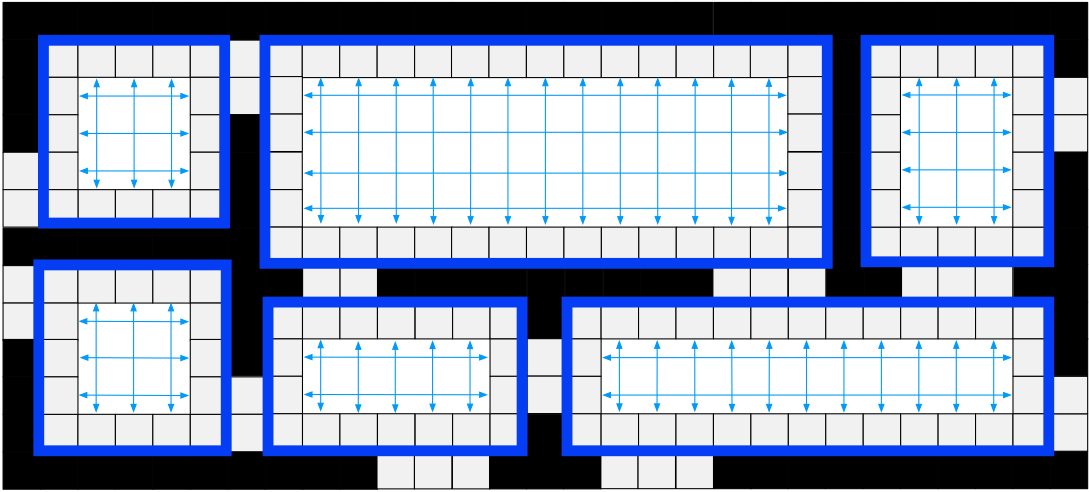
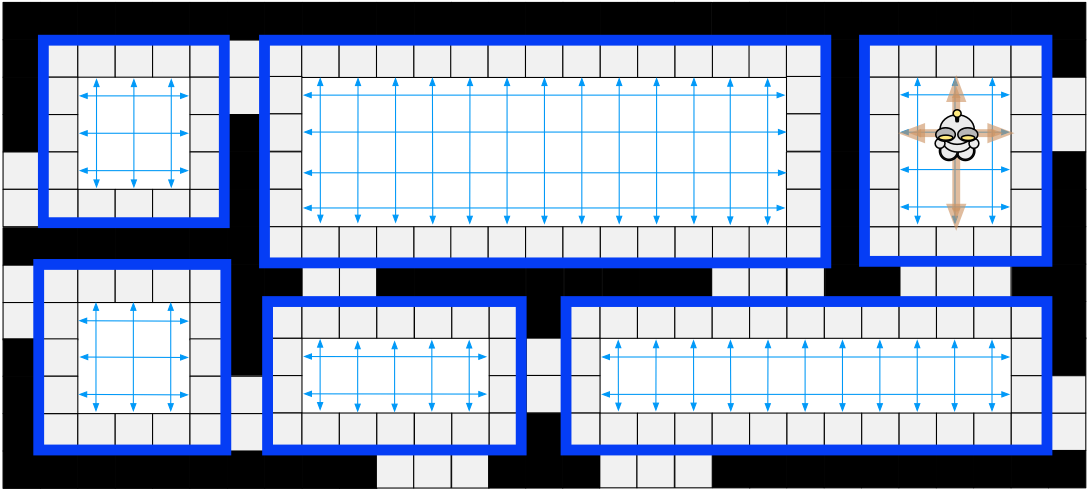
- Part two discusses Rectangular Symmetry Reduction (RSR) [2]: a simple yet effective preprocessing algorithm that eliminates many path symmetries by decomposing a grid map into a set of empty rectangles.
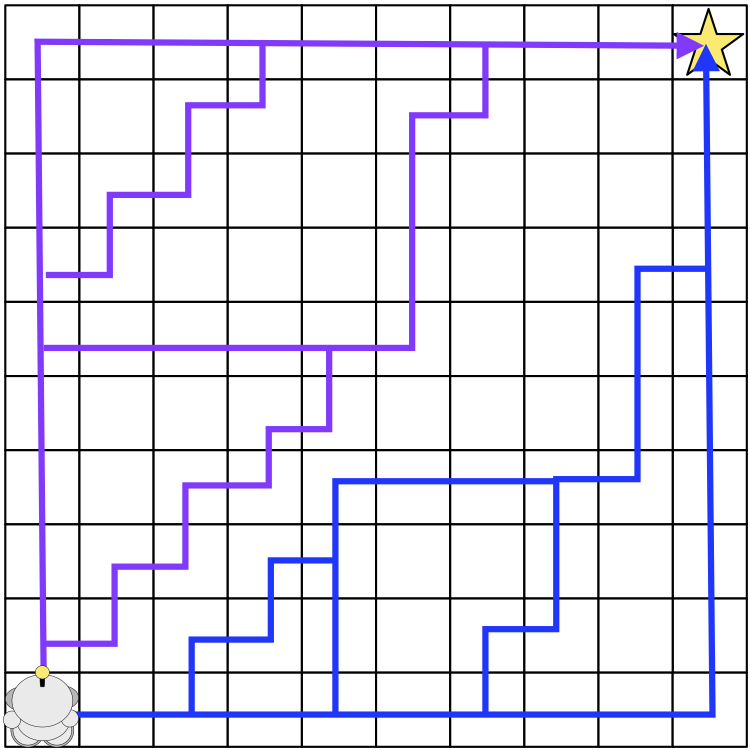
In this article I describe Jump Point Search (JPS) [3]: an online symmetry breaking algorithm which speeds up pathfinding on uniform-cost grid maps by “jumping over” many locations that would otherwise need to be explicitly considered. JPS is faster and more powerful than RSR: it can consistently speed up A* search by over an order of magnitude and more. Unlike other similar algorithms JPS requires no preprocessing and has no memory overheads. Further, it is easily combined with most existing speedup techniques — including abstraction and memory heuristics.
Please note: this work was developed in conjunction with Alban Grastien. It forms part of my doctoral research into pathfinding at NICTA and The Australian National University. Electronic copies of the paper in which this idea was first described are available from my homepage.The Algorithm
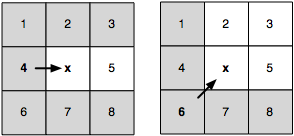
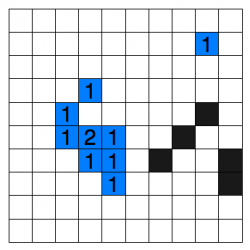
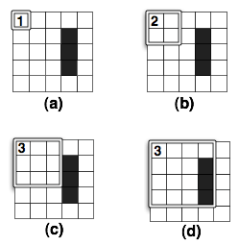
We will refer to the set of nodes that remain after pruning as the natural neighbours of the current node. These are marked white in Figure 1. Ideally, we only ever want to consider the set of natural neighbours during expansion. However, in some cases, the presence of obstacles may mean that we need to also consider a small set of up to k additional nodes (0 ≤ k ≤ 2). We say that these nodes are forced neighbours of the current node. Figure 2 gives an overview of this idea.
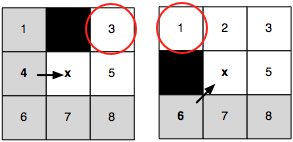
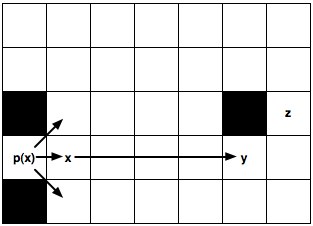
(a) Jumping Straight

(b) Jumping Diagonally
(a) We recursively apply the straight pruning rule and identify y as a jump point successor of x. This node is interesting because it has a neighbour z that cannot be reached optimally except by a path that visits x then y. The intermediate nodes are never explicitly generated or even evaluated.
(b) We recursively apply the diagonal pruning rule and identify y as a jump point successor of x. Notice that before each diagonal step we first recurse straight (dashed lines). Only if both straight recursions fail to identify a jump point do we step diagonally again. Node w, which is simply a forced neighbour of x, is generated as normal.
Properties and Performance
- It is optimal.
- It involves no pre-processing.
- It requires no extra-memory overheads.
- It can consistently speed up A* search by over 10 times; making it not only competitive with, but often better than, approximate techniques such as HPA* [1].
Properties 1-3 are interesting theoretical results, and rather surprising, but I will not address them further here. My main objective in this article is simply provide a flavour for the work; for a full discussion, including proofs, please see the original paper [3]. Property 4 is perhaps of broadest practical interest so I will give a short summary of our findings below.
We evaluated JPS on four map sets taken from Nathan Sturtevant’s freely available pathfinding library, Hierarchical Open Graph. Two of the benchmarks are realistic, originating from popular BioWare video games Baldur’s Gate II: Shadows of Amn and Dragon Age: Origins. The other two Adaptive Depth and Rooms are synthetic though the former could be described as semi-realistic. In each case we measured the relative speedup of A* + JPS vs. A* alone.Briefly: JPS can speed up A* by a factor of between 3-15 times (Adaptive Depth), 2-30 times (Baldur’s Gate), 3-26 times (Dragon Age) and 3-16 times (Rooms). In each case the lower figure represents average performance for short pathfinding problems and the higher figure for long pathfinding problems (i.e. the longer the optimal path to be found, the more benefit is derived from applying JPS).
What makes these results even more compelling is that in 3 of the 4 benchmarks A* + JPS was able to consistently outperform the well known HPA* algorithm [1]. This is remarkable as A* + JPS is always performing optimal search while HPA* is only performing approximate search. On the remaining benchmark, Dragon Age, we found there was very little to differentiate the performance of the two algorithms. Caveat emptor: It is important to highlight at this stage that A* + JPS only achieves these kids of speedups because each benchmark problem set contains a large number of symmetric path segments (usually manifested in the form of large open areas on the map). In such cases JPS can exploit the symmetry and ignore large parts of the search space. This means A* both generates and expands a much smaller number of nodes and consequently reaches the goal much sooner. When there is very little symmetry to exploit however we expect that our gains will be more modest.Screenshots
Final Thoughts
Another exciting aspect of this work is the possibilities it opens for further research. For example: could we pre-process the map and go even faster? Or: are there analogous jumping rules that one could develop for weighted grids? What about other domains? Could we apply the lessons learned thus far to help solve other interesting search problems? The answers to the first two questions already appear to be positive; the third is something I want to explore in the near future. Regardless of how it all turns out, one thing is certain: it’s an exciting time to be working on pathfinding!